Regression-based Physics Informed Nueral Networks for Magentopause Tracking

Abstract

The ultimate goal of studying the magnetopause position is to accurately determine its location. Both traditional numerical computation methods and the currently popular machine learning approaches have shown promising results. In this study, we propose a Regression-based Physics-Informed Neural Networks (Reg-PINNs) that combines physics-based numerical computation with vanilla machine learning. This new generation of PINNs overcomes the limitations of previous methods restricted to solving ordinary and partial differential equations by incorporating conventional empirical models to aid the convergence and enhance the generalization capability of the neural network. Compared to Shue et al. [1998], our model achieves a reduction of approximately 30% in root mean square error.

Introduction

Magnetopause Tracking

The boundary where the solar wind dynamic pressure is balanced by the magnetic pressure of Earth’s magnetosphere.
Major controlled by IMF
\[Bz\]
& $Dp$

Comparison of nowadays methods for magnetopause tracking and the proposed Reg-PINNs.

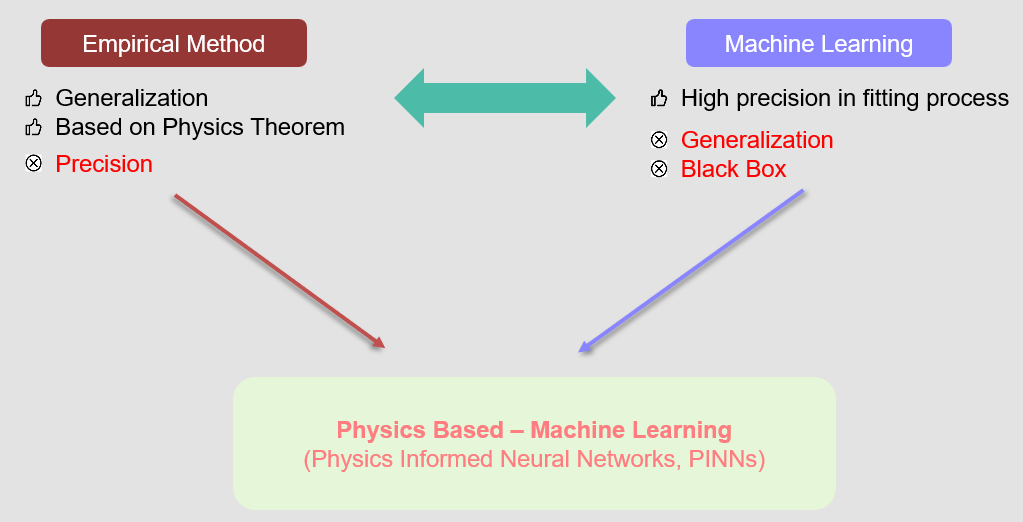
Currently, there is a lack of models that can simultaneously address the aforementioned issues. Therefore, we propose a new generation of Physics Informed Neural Networks (PINNs) named Reg-PINNs.

Dataset

A total of 34,998 magnetopause in-situ crossing data points were included in the analysis, derived from various sources such as THEMIS (28,634), Geo-Tail (5,764), ISEE, IMP 8, among others. For each data point, the corresponding time stamps were identified, and the 5-minute averages were calculated using the OMNI dataset recorded at five-minute intervals. In order to enable the empirical model to generalize within a specific region, we integrated the collected data from the same bin. Each bin encompasses north-south interplanetary magnetic field (IMF $Bz$) values spanning across 3 values, with a shift of 1 $Bz$ for each subsequent bin. Additionally, each bin includes 2 values of solar wind dynamic pressure ($Dp$), with a shift of 0.5 $Dp$ for each subsequent bin. The range of the dataset used in this study is consistent with that of Shue et al. [1998], which is -18 nT < $Bz$< 15 nT and 0.5 nPa < $Dp$ < 8.5 nPa. Figure 1i displays the distribution of X-GSM and Y-GSM coordinates in the GSM coordinate system for the Geo-Tail data. On the other hand, Figure 2 illustrates the range of distribution for $Dp$ and $Bz$ variables.

<br>

There are a total of 34,998 magnetopause in-situ crossing data points. (THEMIS(28634), Geo-Tail(5764), ISEE, IMP 8, etc.)
Applying the OMNI dataset recorded every five minutes, identify the corresponding time stamps and calculate the 5-minute averages.

Methodology

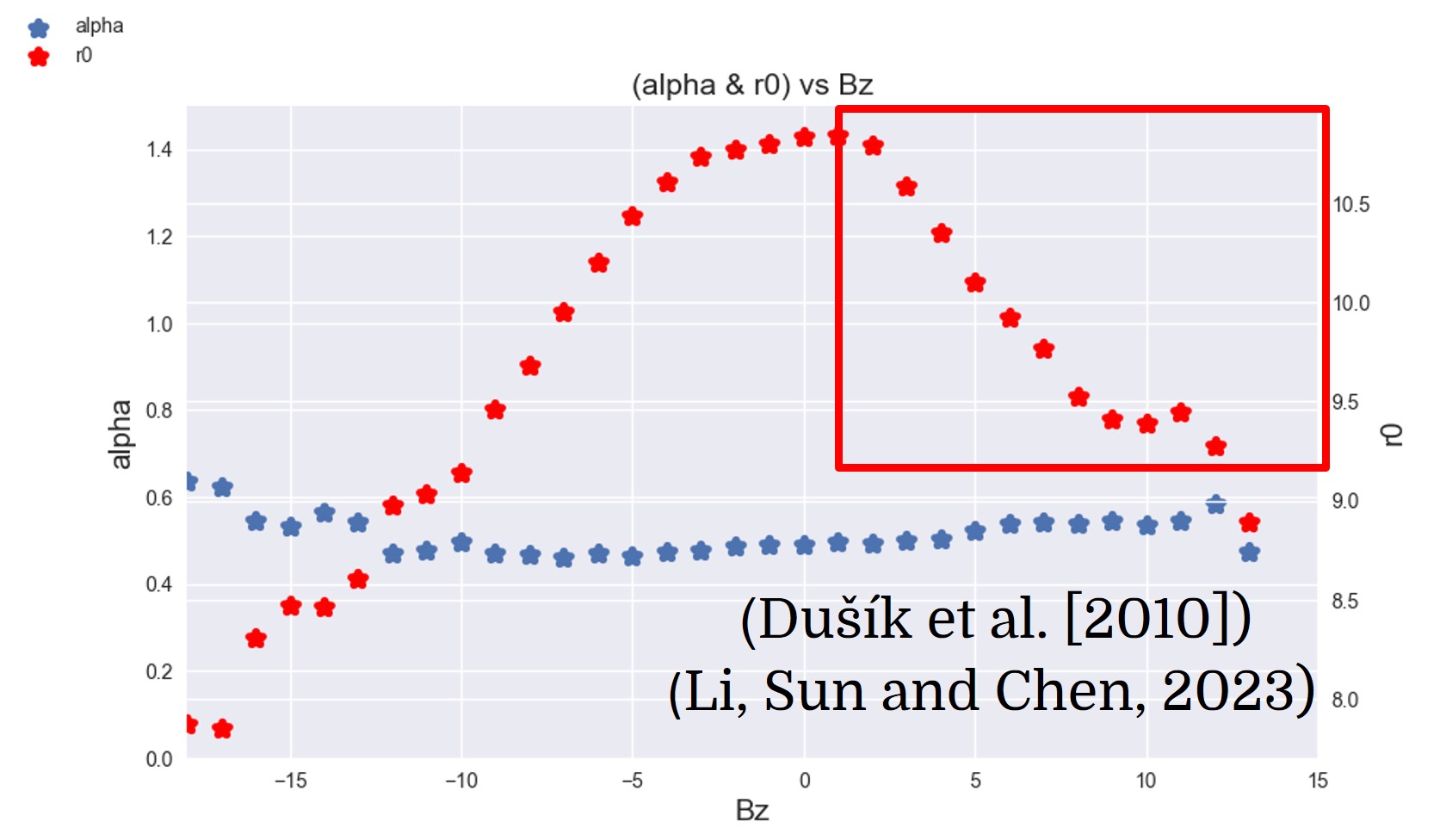
We inherit the function form proposed by Shue et al. [1997] and re-evaluate the relationship between Bz and Dp with respect to $r_0$ and 𝛼. Additionally, we propose an alternative parameter-based numerical model.

\[r = r_0 \left(\frac{2}{1 + \cos \theta}\right)^\alpha\]

Proposed Parameters

\[r_0 = \left(9.332 + 1.308 \cdot \tanh\left(0.213 \cdot (B_z + 11.191) - 0.568 \cdot \tanh\left(0.479 \cdot (B_z - 7.188)\right)\right)\right) \cdot (D_p)^{\left(-\frac{1}{6.22}\right)}\] \[\alpha = \left(0.493 - 3.5 \times 10^{-4} \cdot B_z\right) \cdot (D_p)^{\left(\frac{1}{11.92}\right)}\]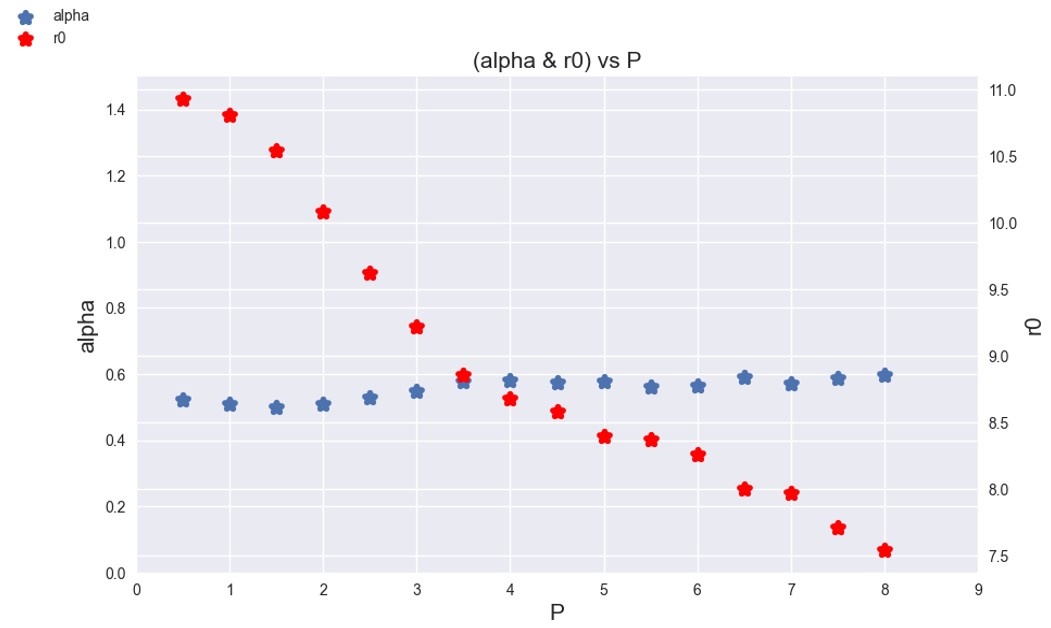

(r_0 and 𝛼) vs. Pressureand (r_0 and 𝛼) vs. IMF B_z

Proposed Neural Network Architecture

The inspiration for the model proposed in this study originates from the use of Physics Informed Neural Networks (PINNs) for solving high-resolution spatio-temporal simulations, where partial differential equations (PDEs) and other physical equations guide the model to achieve generalization. However, previous literature does not mention the use of algebraic equations for guiding the model. Therefore, we propose incorporating the results obtained from physically meaningful algebraic models to guide the neural network. This novel approach is referred to as Regression-based-PINNs, abbreviated as Reg-PINNs

Functional Flow Block Diagram of Reg-PINNs

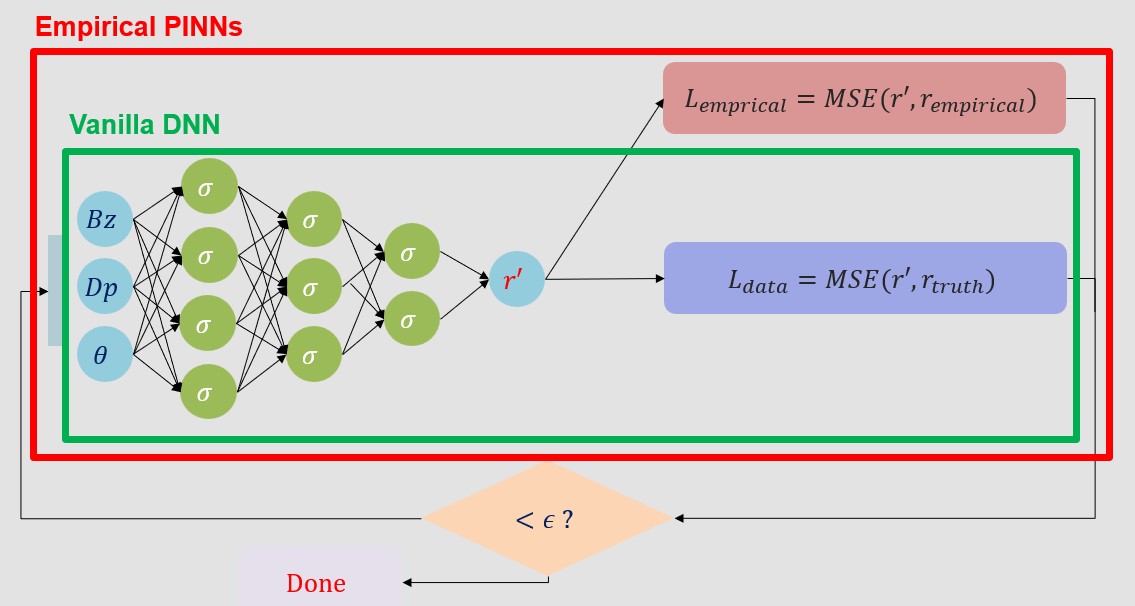
Algorithm

Results

Numerical-Based Model Results {Shue et al[1998], Proposed Model}

Table 1. Proposed numerical model performance evaluation

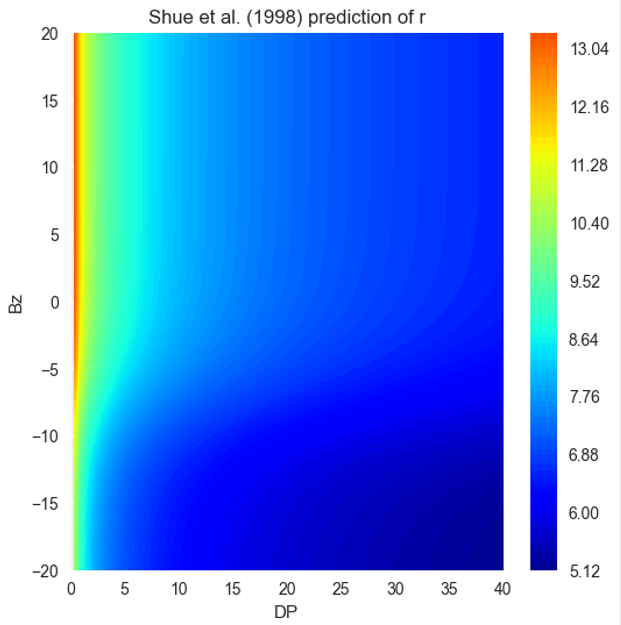
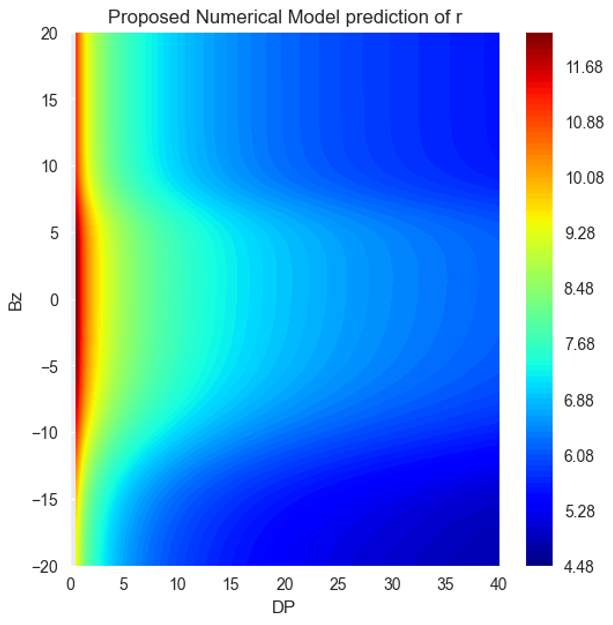
In Table 1, three rules of thumb are provided. Shue et al. [1998] is used as the baseline, and it can be observed that both the proposed empirical model and MCMC show slight improvements compared to the baseline.

Machine Learning Methods Results {Vanilla Neural Network, Reg-PINNs(Shue et al[1998]), Reg-PINNs(Proposed Numerical-based Model)}

Table 2. Reg-PINNs model performance evaluation

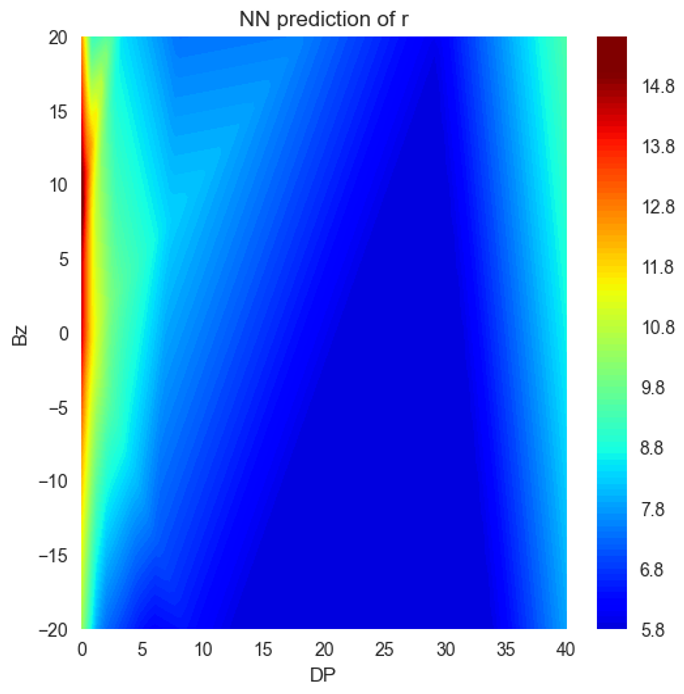
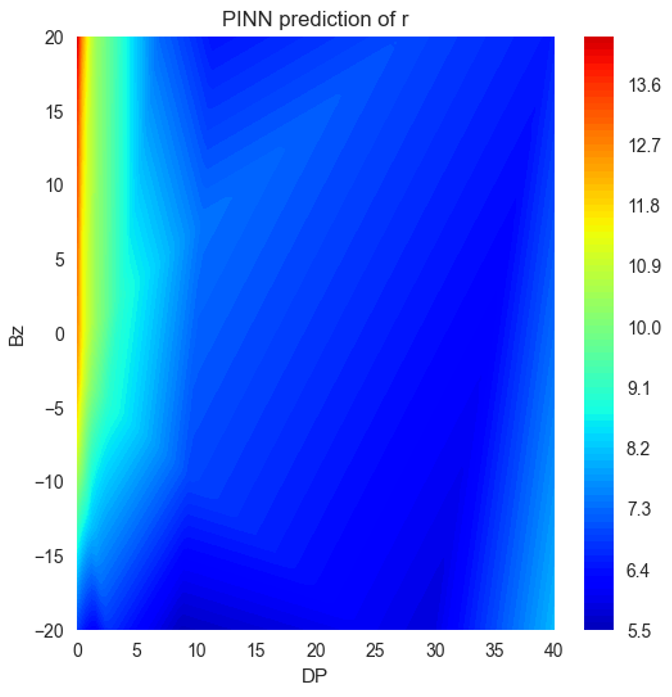
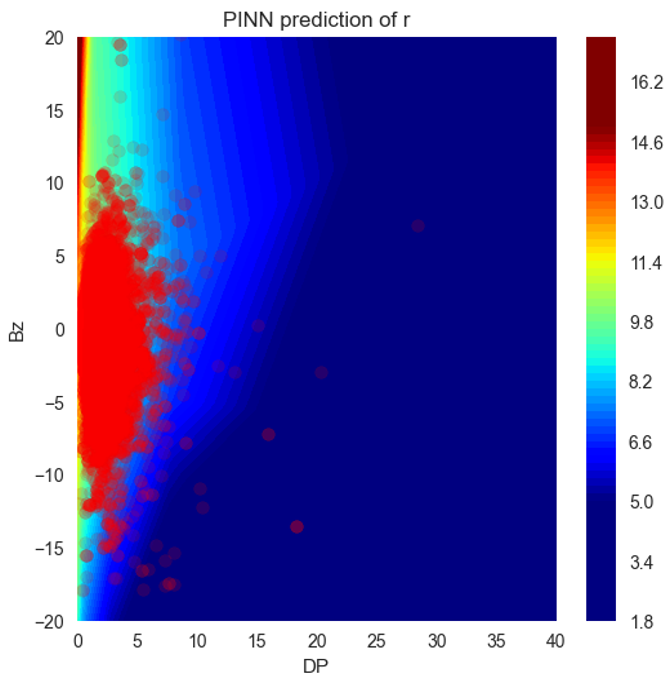
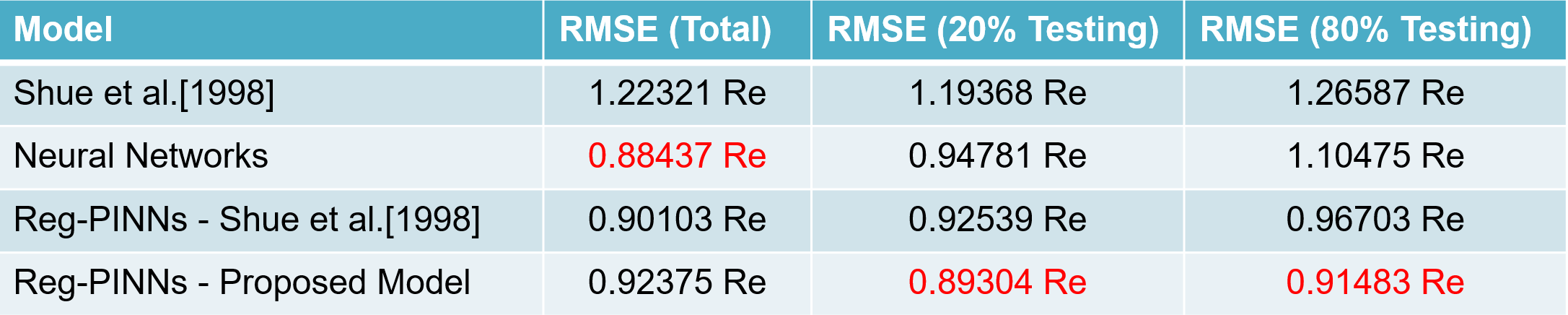
In Table 2, we compare the evaluation of Neural Networks-based models using three types of datasets. The first type involves training the model using all the available data. The second type involves training the model using 80% of the data, and the last type involves training the model using 20% of the data.

Loss v.s. Iteration

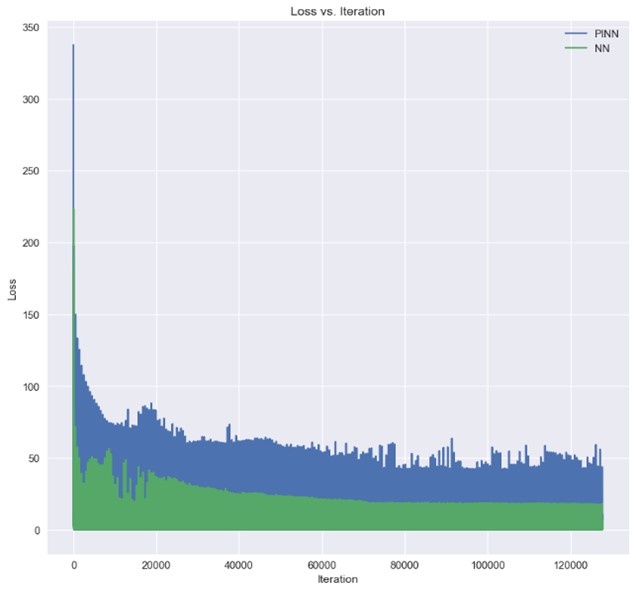
When comparing the training loss, we observe that

\[L_{NN} < L_{PINN} < L_{Empirical}\]

. This is because Reg-PINN incorporates the residual of the guiding formula during gradient descent, making the loss higher compared to NN, as shown in the below graph. Therefore, when evaluating RMSE using the entire dataset, we can see that Neural Network achieves the lowest error. However, as mentioned earlier, machine learning has limited generalization capabilities. Therefore, when introducing the empirical formula, we can observe a significant discrepancy between Reg-PINN, NN, and Shue et al. [1998] in the case of 20% and 80% unseen data. Reg-PINN exhibits robustness and consistently superior accuracy performance compared to NN when evaluated on 20% and 80% unseen data.

RMSE in Shue’s applicable region

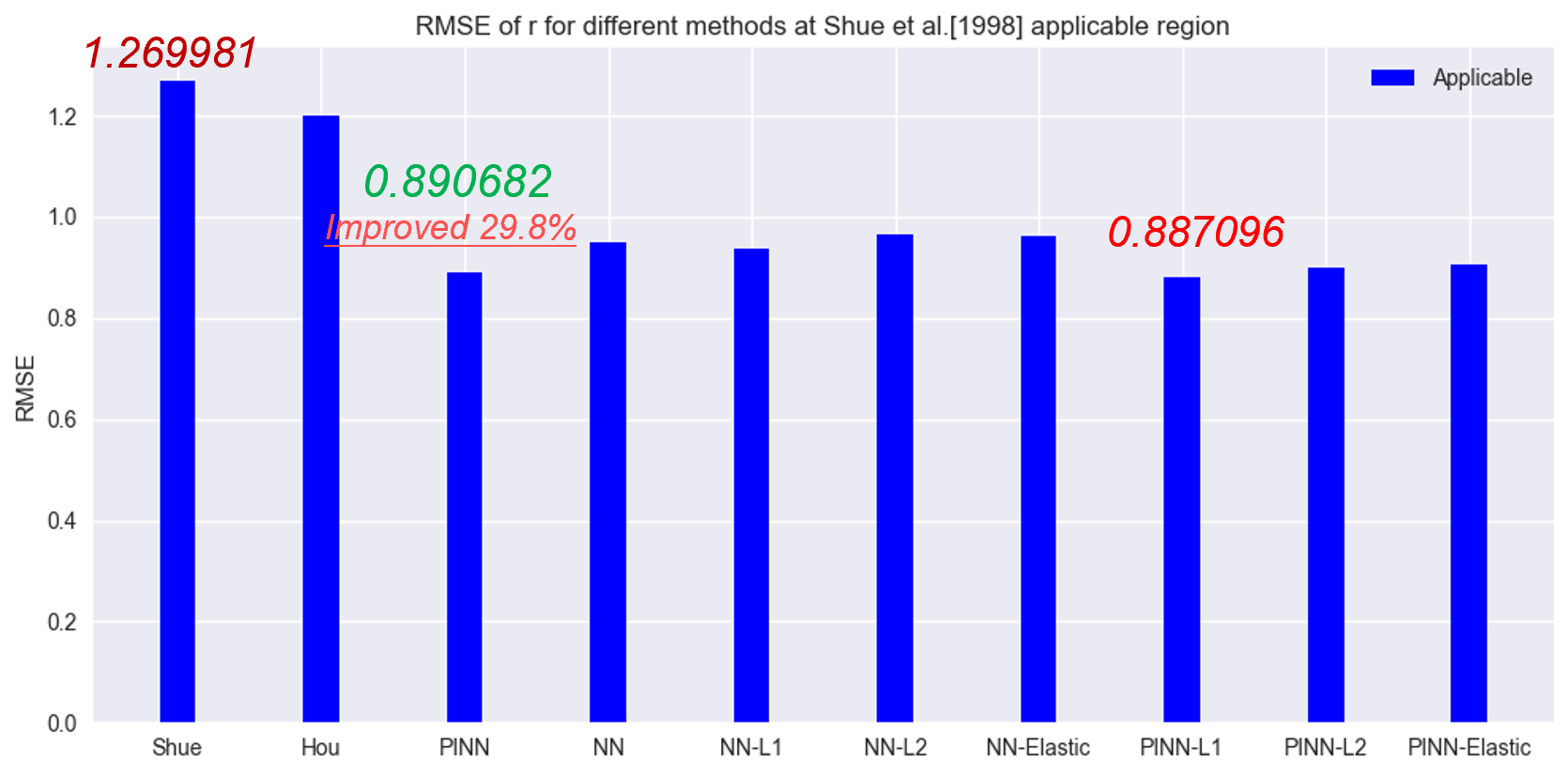
We test the data points within the applicability range of Shue et al. [1998]. It is evident that the empirical model is unable to compete with the neural network models, while Reg-PINN, benefiting from the guidance of the empirical formula, is less affected by extreme values, allowing the model to generalize well and maintain high accuracy. The RMSE value for Reg-PINN in above figure is 0.890682, while for Shue et al. [1998], it is 1.269, indicating a reduction in RMSE of approximately 29.8% for Reg-PINN. Notably, the best-performing model in this case is Reg-PINN + $L_1$ with a value of 0.887. This can be attributed to the $L_1$ regularization, which encourages some weights to approach or equal zero, preventing overfitting and enhancing the model’s generalization ability. According to the T-test results, we calculated that the p-value for the proposed empirical model, Reg-PINN, compared to Shue et al. [1998] is much smaller than 0.005, indicating a significant difference in the means. On the other hand, the average values between Reg-PINN and NN are closer, with a p-value of 0.698. This suggests that Reg-PINNs is indeed a more accurate and generalizable model constructed based on NN.

RMSE in different region of angle

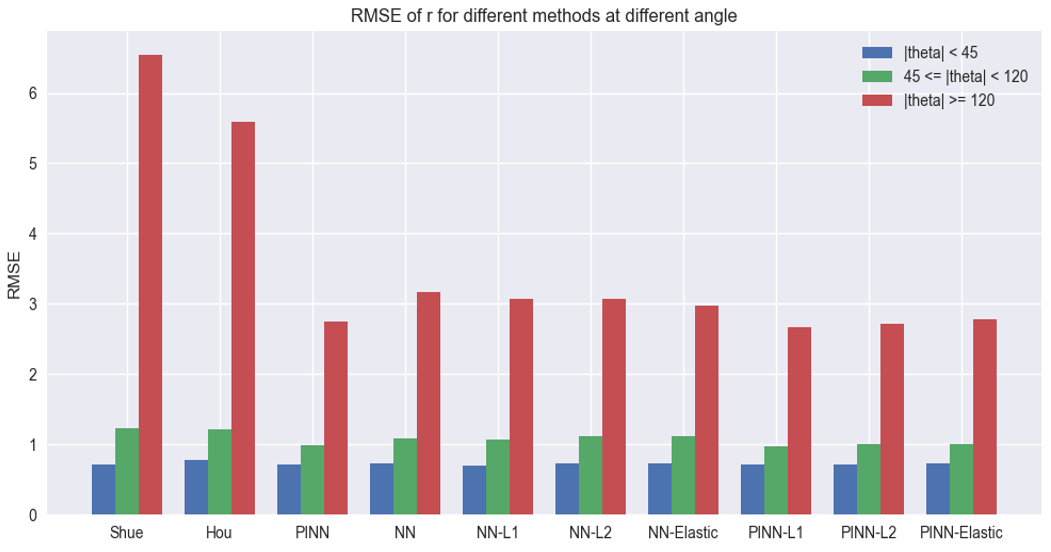
The above graph reveals the evaluation of different angular segments (

\[\|{\theta}\| < 45, 45 ≤ \|{\theta}\| ≤ 120, \|{\theta}\| > 120\]

). It is clear that both the Shue model and the proposed empirical model exhibit significant errors in distance estimation for large opening angles. On the other hand, both the NN and the Reg-PINN perform well, with Reg-PINN outperforming NN. For angles smaller than 120 degrees, the performance of all models does not vary significantly.

RMSE in different region of Bz.

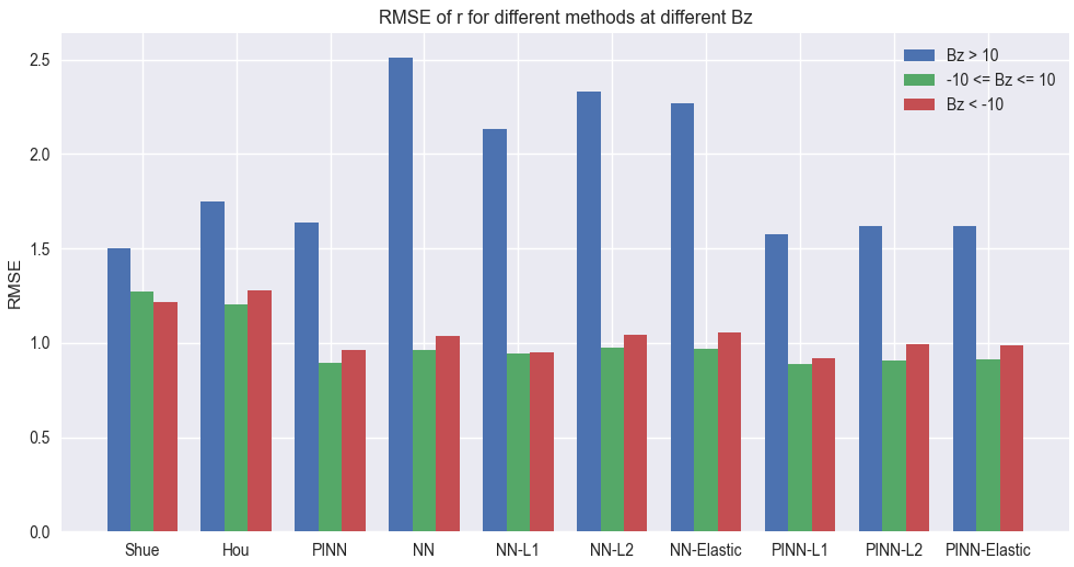
We then investigate the ability of the models to handle stronger $Bz$ values and their sensitivity to the north-south interplanetary magnetic field. In the above figure, it is observed that all types of neural network models perform well when $Bz$ < 10 nT. However, as the northward interplanetary magnetic field strength increases, the NN model exhibits significant errors, while Reg-PINN, guided by the empirical formula, maintains low errors even at $Bz$ > 10 nT. Overall, Reg-PINN performs the best in this scenario.

RMSE in different region of Dp .

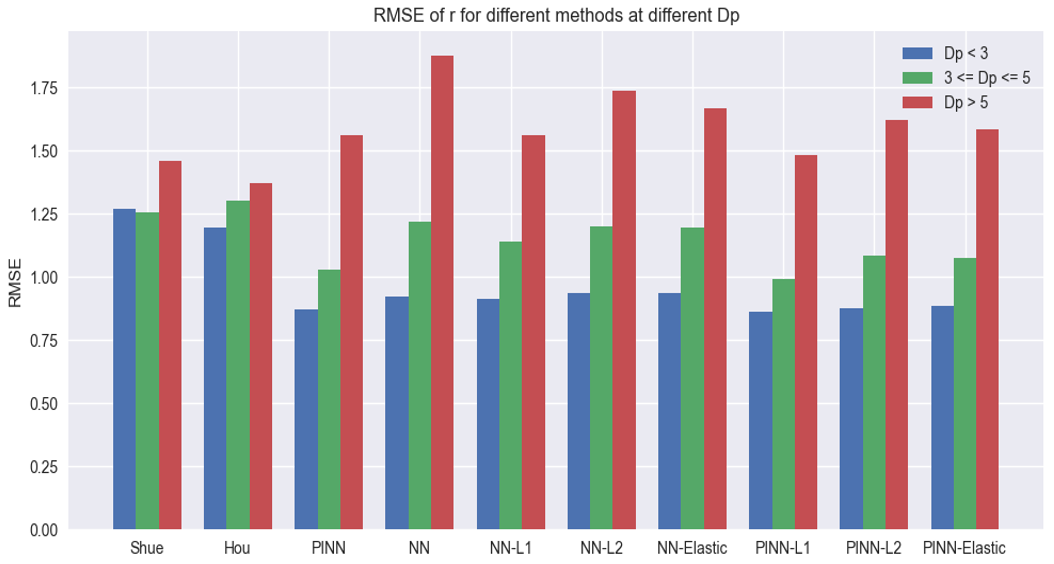
We aim to explore the errors of various models under different solar wind dynamic pressures ($Dp$ < 3 nPa, 3 nPa ≤ $Dp$ ≤ 5 nPa, $Dp$> 5 nPa). It is evident that as Dp increases, the errors of neural network models also increase. Although they perform reasonably well for $Dp$ < 5 nPa, only PINN + $L_1$ regularization can compete with Shue et al. [1998] when $Dp$ > 5

Conclusion

We re-evaluate the relationship between parameters ($Bz$, $Dp$) and $r_0$ and $\alpha$, and propose alternative types of numerical models.
The proposed algorithm (Reg-PINNs) resolves the issues of numerical methods’ inherent lack of precision and the poor generalization capabilities of machine learning.
Reg-PINNs is an algorithm that constrains vanilla neural networks to converge on predictions and enhances generalization by excluding intervening outliers.
Reg – PINNs is capable of handling multivariate input and multivariate output. However, in this study, we only focus on discussing the prediction of magnetopause locations in the space domain, considering multivariate inputs and a single output.
The proposed Reg-PINNs introduced in this study allows the incorporation of algebraic equations for model training, expanding the capabilities of traditional PINNs, which primarily focus on solving ordinary and partial differential equations (ODEs and PDEs).
Reg-PINNs greatly improve the model’s performance in predicting the location of the Magnetopause, achieving a remarkably improvement of 29.8 %.
$L_1$ (Lasso), $L_2$ (Ridge), and Elastic regularization techniques show a significant improvement in predicting the variable $r$ when $Bz$ varies.. $$
Reg-PINNs significantly improves the precision within the applicable scope of Shue et al. [1998].

References

Shue, J.-H. et al. (1997) ‘A new functional form to study the solar wind control of the magnetopause size and shape’, Journal of Geophysical Research: Space Physics, 102(A5), pp. 9497–9511. Available at: https://doi.org/10.1029/97JA00196.
J.-H. Shue et al. (1998) ‘Magnetopause location under extreme solar wind conditions’, Journal of Geophysical Research: Space Physics, 103(A8), pp. 17691–17700. Available at: https://doi.org/10.1029/98JA01103.
Dusik, S., et al. (2010). THEMIS observations of magnetosheath‐like plasma in the near‐Earth magnetotail. Journal of Geophysical Research: Space Physics, 115(A12), A12223. https://doi.org/10.1029/2010JA015681
Raissi, M., Perdikaris, P. and Karniadakis, G.E. (2019) ‘Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations’, Journal of Computational Physics, 378, pp. 686–707. Available at: https://doi.org/10.1016/j.jcp.2018.10.045.
Li, S., Sun, Y.-Y. and Chen, C.-H. (2023) ‘An Interpretable Machine Learning Procedure Which Unravels Hidden Interplanetary Drivers of the Low Latitude Dayside Magnetopause’, Space Weather, 21(3), p. e2022SW003391. Available at: https://doi.org/10.1029/2022SW003391

Acknowledgements

We would like to express my heartfelt appreciation to NCHC – NARLabs, for providing the computation resource from TAIWANIA-2. Additionally, I would like to extend my gratitude to Mr. Yu-Wei Chen and Mr. Pai-Sheng Wang, Researchers at the Space Environment Laboratory – NCU, for their contribution in reinforcing the understanding of magnetopause.