Pretrained Fourier Neural Operator for Non-Newtonian Fluid Dynamics

Disclaimer

The dataset presented in this project is generated from the Moldex3D simulation software, which is a commercial software for simulating the injection molding process. The dataset is not publicly available, and the results are for demonstration purposes only. The project is a proof-of-concept to apply the Fourier Neural Operator (FNO) to learn and infer the physical mode in mold flow analysis. The project is not intended for commercial use or any other purposes.

Abstract

The project applies the Fourier Neural Operator (FNO) from ICLR 2021, “Fourier Neural Operator for Parametric Partial Differential Equations,” to learn and infer the physical mode in mold flow analysis. FNO is a data-driven approach to solving PDEs in mapping the function in Fourier function spaces rather than finite-dimensional Euclidean spaces. The goals of the project are to learn the physical mode of non-Newtonian fluid dynamics and to predict the pressure (with a MAE of less than 3 Pa) and Melt Front Time (with a MAE of less than 0.3 s).

Fourier Neural Operator (FNO)

Fourier Neural Operator (FNO) is a data-driven approach to solving PDEs in mapping the function in Fourier function spaces, which is infinite-dimensional, rather than finite-dimensional Euclidean spaces. The first step of the FNO model is to project the input data to high-dimensional Fourier space, then eliminate the high-frequency components and add the residual part, and finally map the data back to the original space. The FNO model is defined as:

Definition 1 (Iterative updates) Define the update to the representation \(v_t \rightarrow v_{t+1}\) by

\[v_{t+1}(x) := \sigma(Wv_t(x) + (K(\alpha; \phi)v_t)(x)), \quad \forall x \in D\]

Definition 2 (Kernel integral operator \(K\)) Define the kernel integral operator mapping by

\[(K(\alpha; \phi)v)(x) := \int_D k(x, y, \alpha(x), \alpha(y)) \phi(v(y)) dy, \quad \forall x \in D\]

Definition 3 (Fourier integral operator \(K\)) Define the Fourier integral operator

\[(K(\phi)v)(x) := F^{-1}(R_{\phi} \cdot (Fv))(x), \quad \forall x \in D\]

The Fourier transform and its inverse are defined respectively as:

\[(\mathcal{F}f_j)(k) = \int_D f_j(x) e^{-2\pi i k \cdot x} \, dx\] \[(\mathcal{F}^{-1}f_j)(x) = \int_D f_j(k) e^{2\pi i k \cdot x} \, dk\]

which can be illustrated in the following diagram:

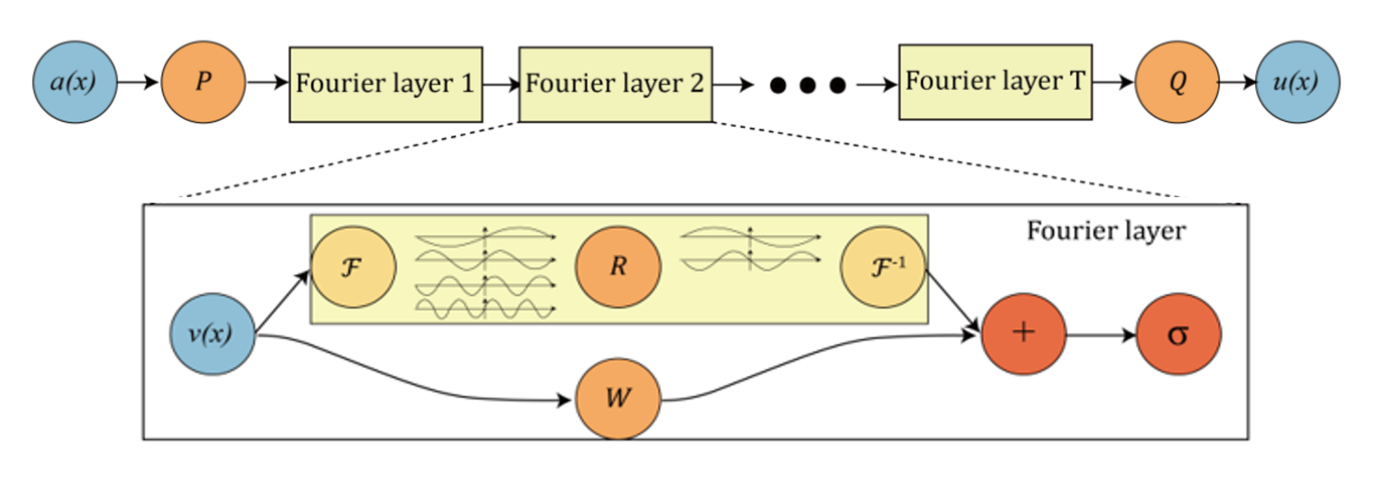
FNO Functional Flow Block Diagram

Credit: arXiv:2010.08895

Dataset

The dataset is generated from the Moldex3D simulation software, which is a commercial software for simulating the injection molding process. The dataset consists of 45 runs of mold flow analysis, each having 456391 data points in a 3D plastic injection molding machine, which is a typical geometry in the injection molding process. The dataset includes the following condtions and features in the same geometry of the injection molding machine: [cooling_time, filling_speed, VP_position, packing_pressure_1, packing_pressure_2, packing_pressure_3, packing_time_1, packing_time_2, packing_time_3, tube_temperature, mold_temperatire, weight]

The target variables are the pressure and Melt Front Time (MFT). The pressure is the pressure of the plastic in the mold cavity, and the MFT is the time for the plastic to fill the mold cavity.

The dataset is split into 40 runs for training and 5 runs for testing. The training dataset is used to train the FNO model, and the testing dataset is used to evaluate the model performance.

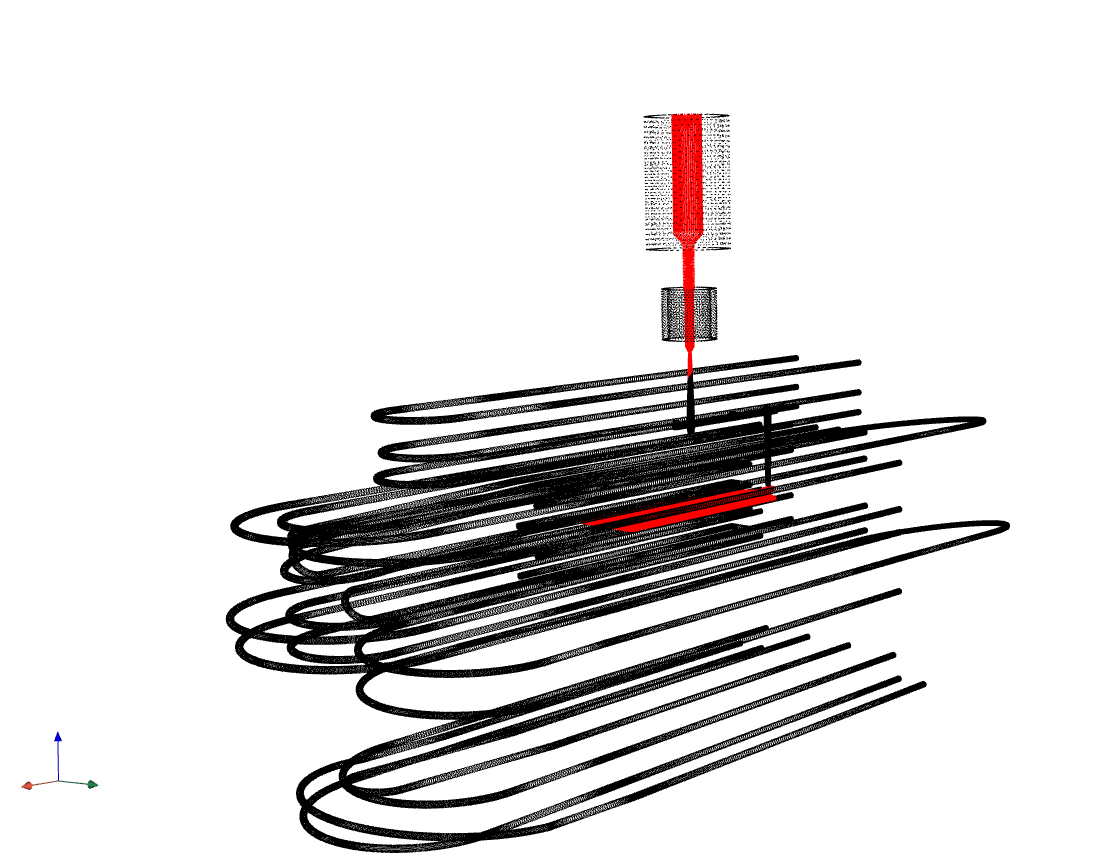
Geometry of the Injection Molding Machine

Results

The results of the project are to predict the pressure and Melt Front Time (MFT) in the injection molding process. The model is trained with the FNO model, and the results are evaluated with the Mean Absolute Error (MAE) metric.

Pressure Prediction

Testing MAE: 2.92408 Pa
Testing MSE: 13.77572 Pa

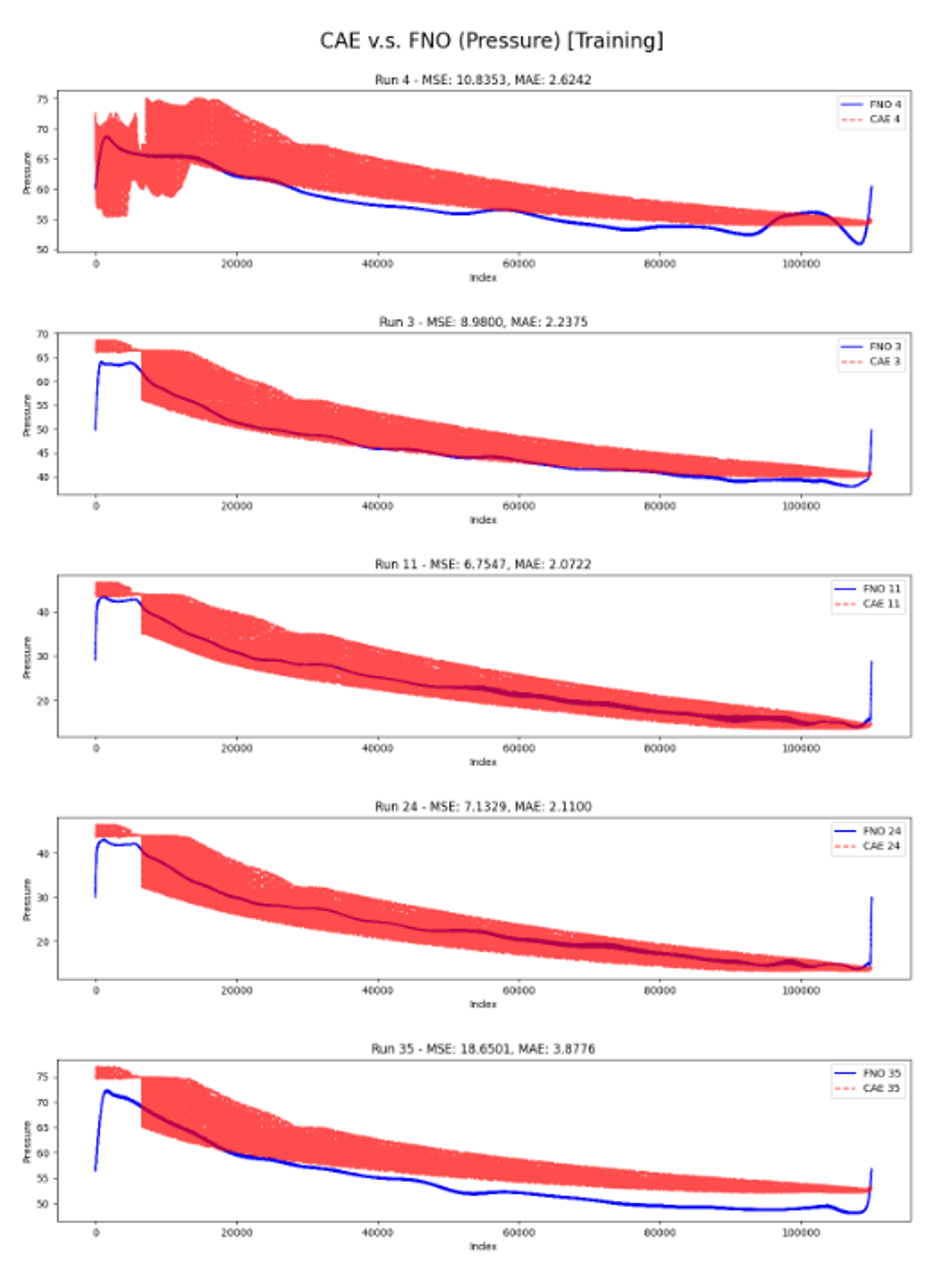
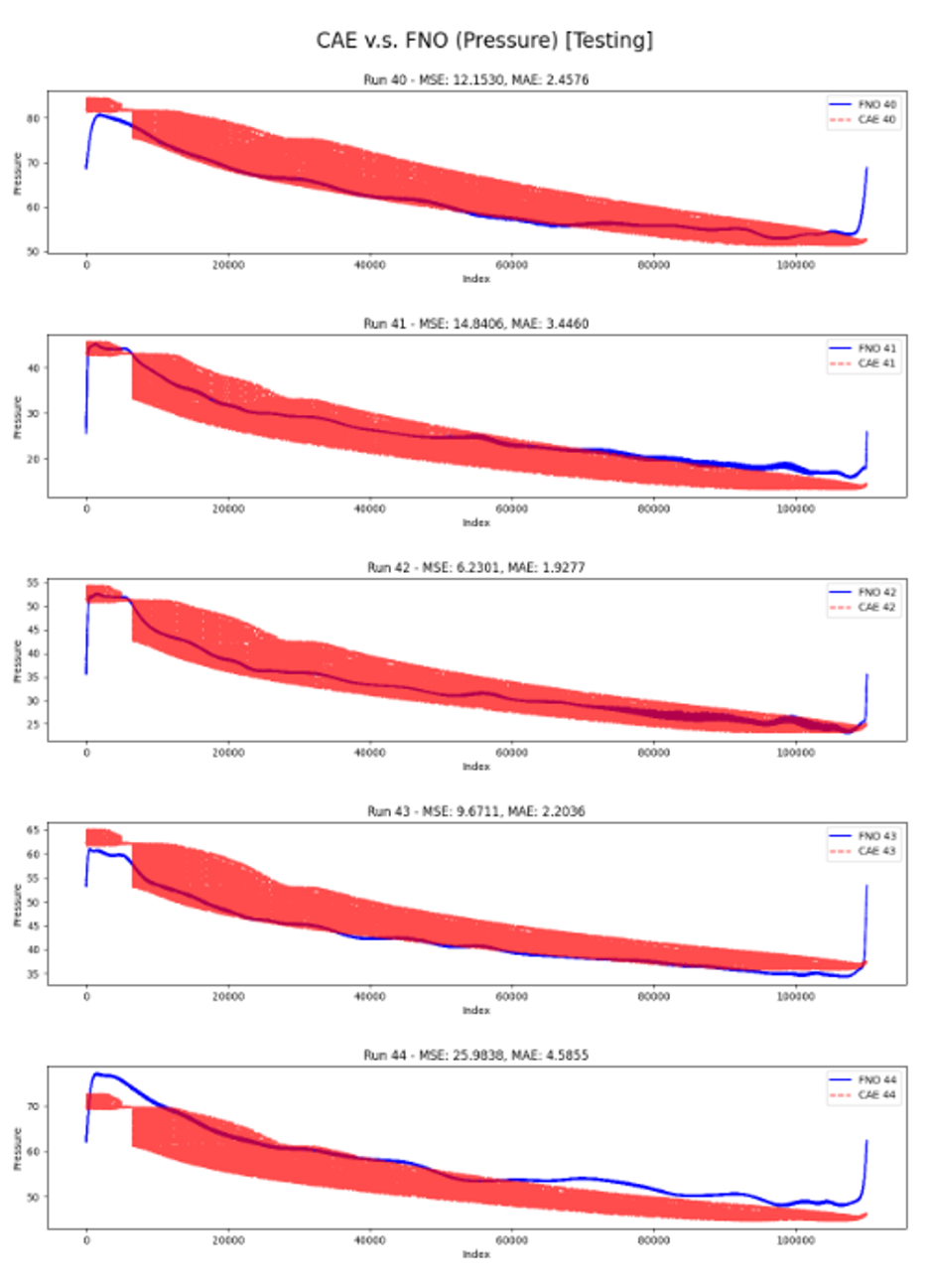
Left: Pressure Prediction in Training, Right: Pressure Prediction in Testing

Red: CAE Solution, Blue: FNO Prediction

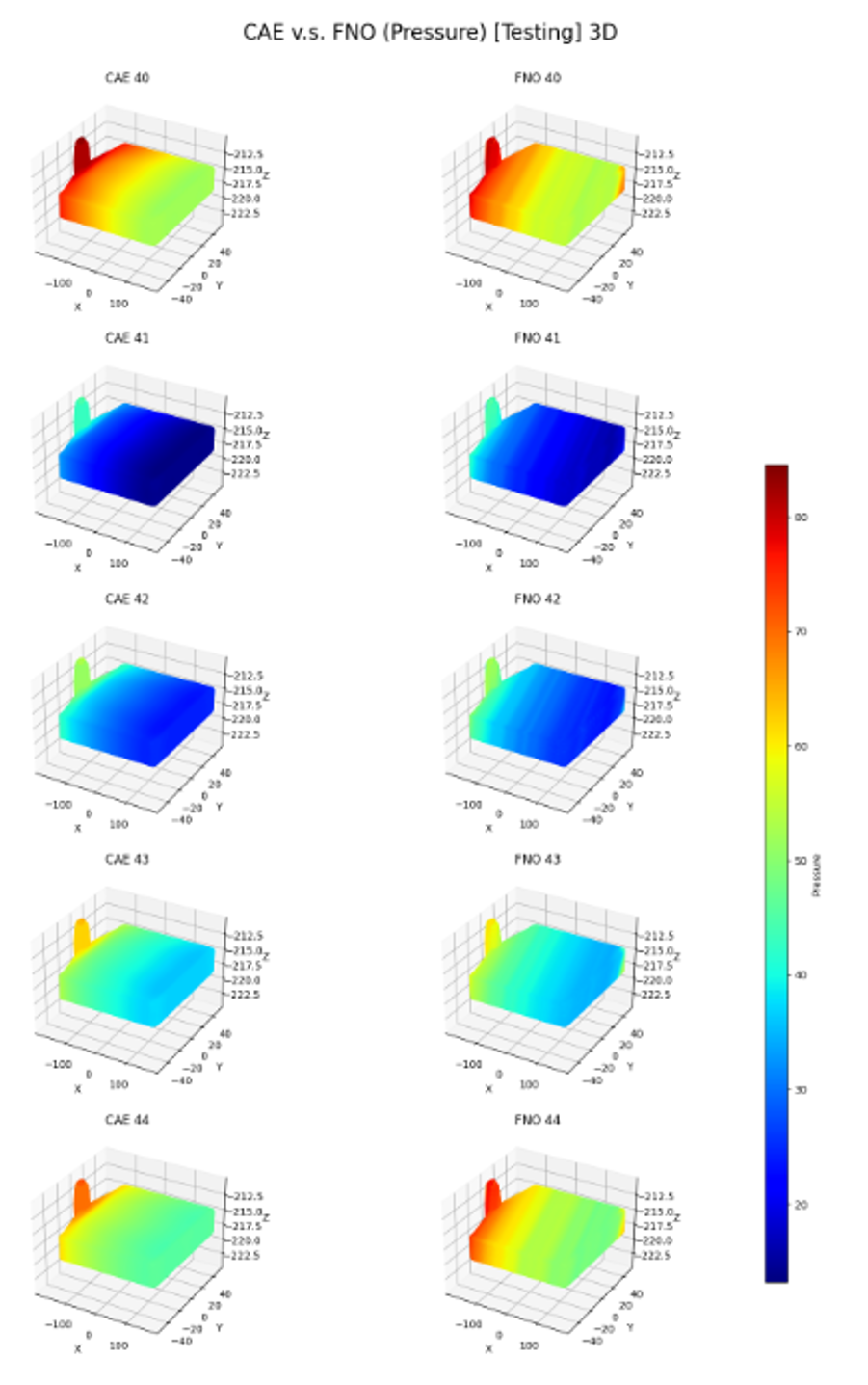
3D plot of CAE Solution and FNO Prediction

Melting Front Time (MFT) Prediction

Testing MAE: 0.24002 s
Testing MSE: 0.00895 s

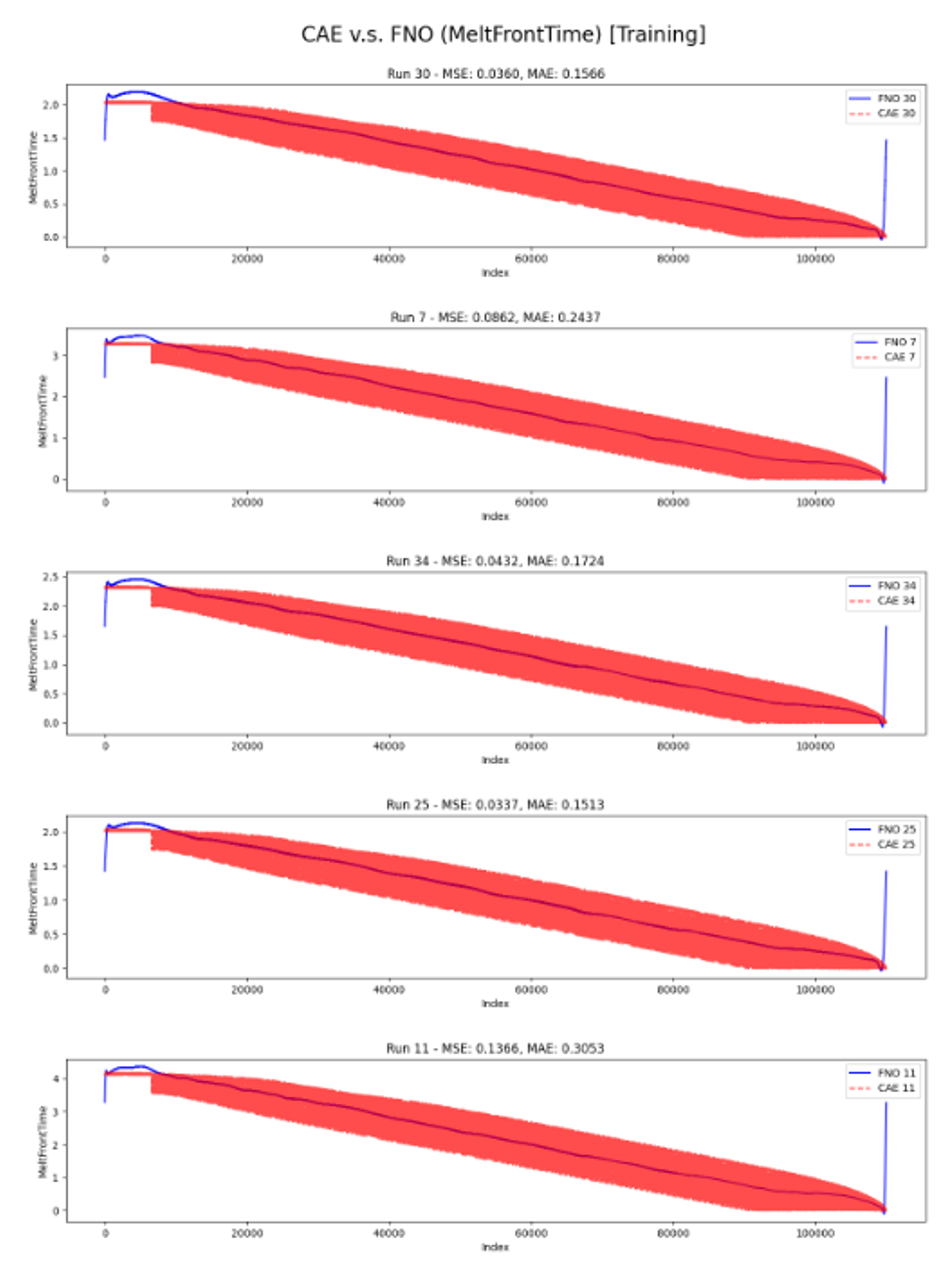
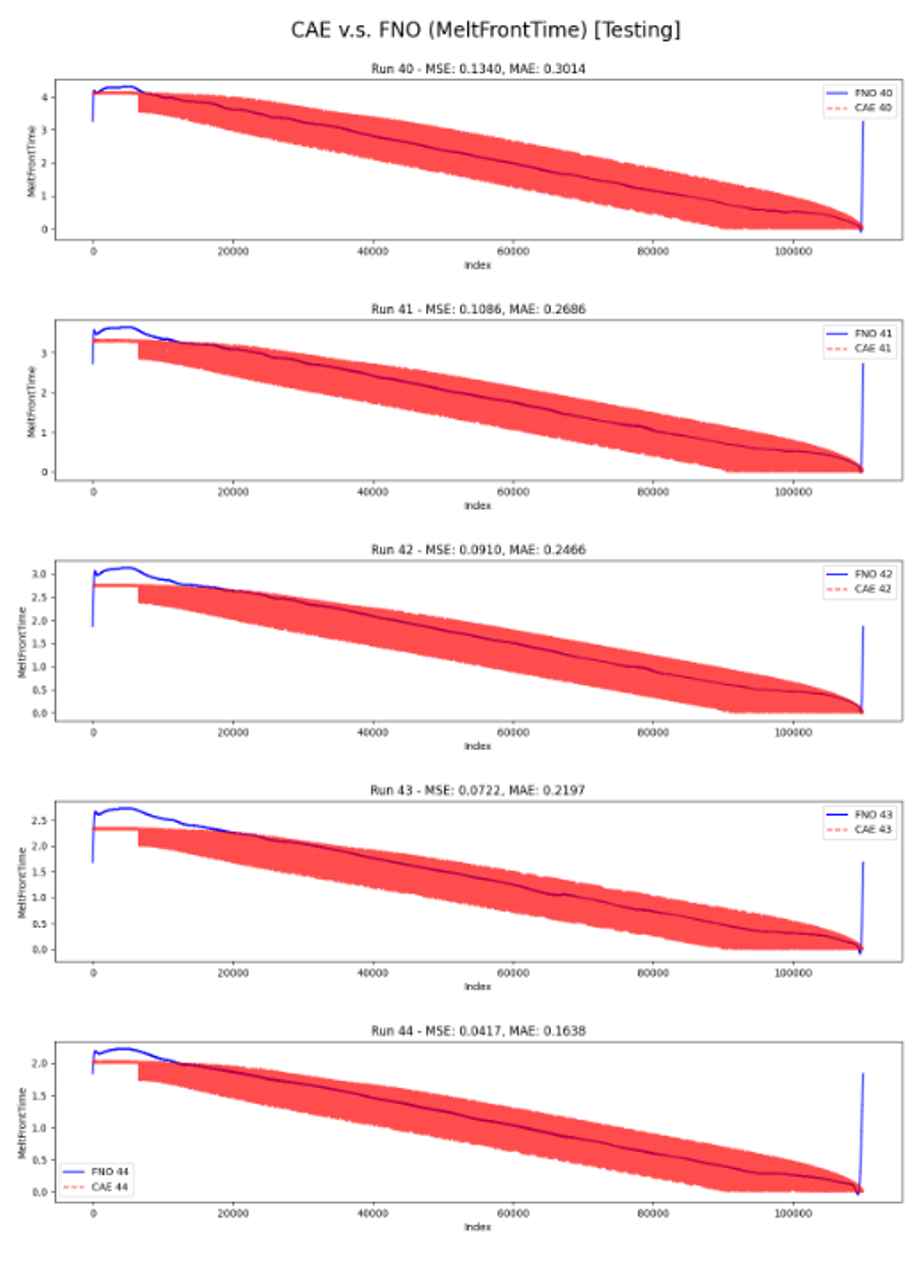
Left: MLT Prediction in Training, Right: MLT Prediction in Testing

Red: CAE Solution, Blue: FNO Prediction

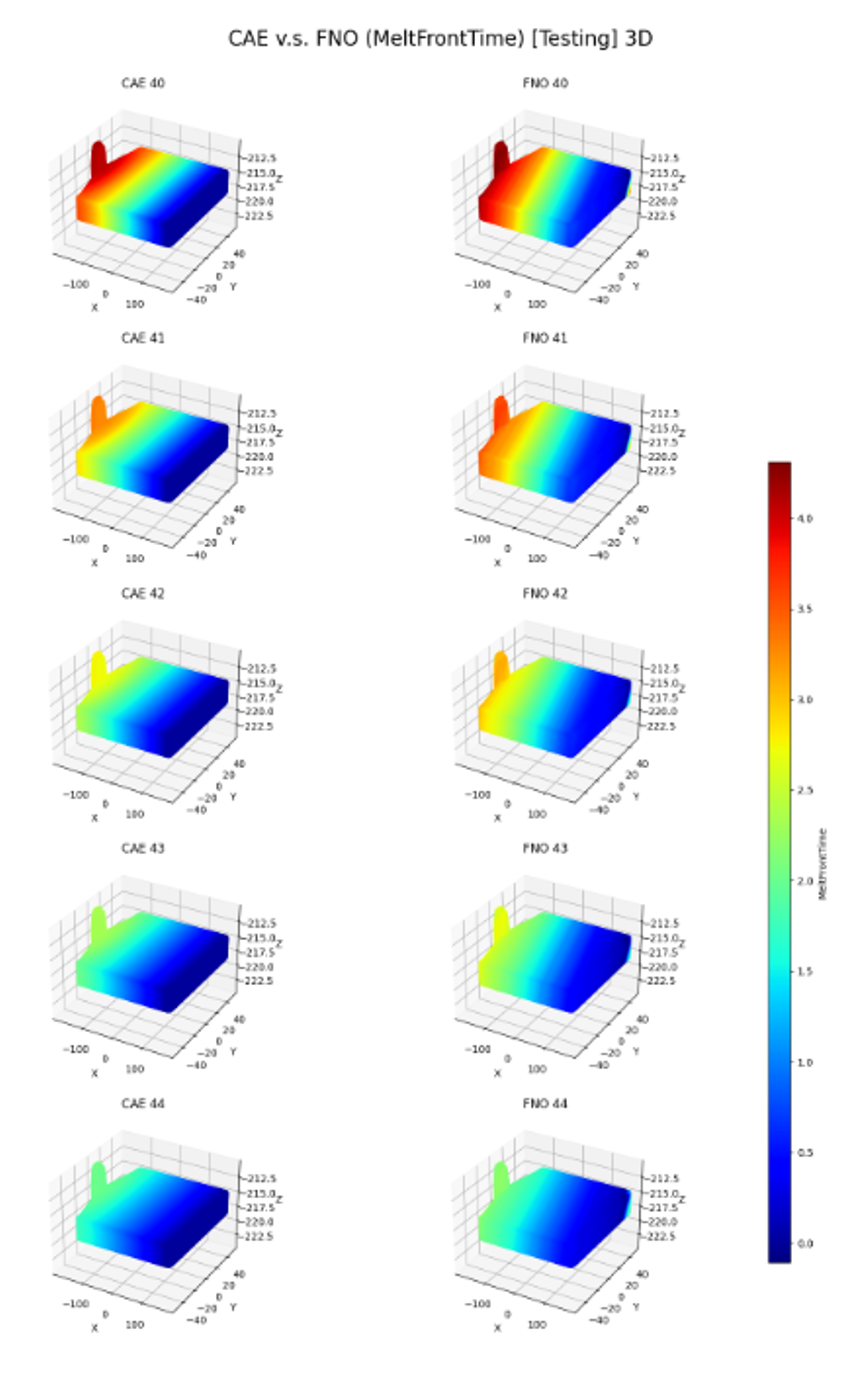
3D plot of CAE Solution and FNO Prediction

Conclusion

In this project, it is evident that the FNO model has the potential to capture the physical mode of non-Newtonian fluid dynamics in the injection molding process. The model can predict the pressure and Melt Front Time (MFT) with a Mean Absolute Error (MAE) of less than 3 Pa and 0.3 s, respectively. We can even observe that the FNO predicts almost on par with the average oscillation produced by CAE numerical simulations. Furthermore, the model’s performance can be further improved by tuning the hyperparameters and increasing the training dataset. This improvement is evident from both the training and testing results, which help to eliminate the spikes in the prediction.

Acknowledgements

We would like to thank the Moldex3D R&F team for providing the dataset and the Moldex3D software for the simulation. Also, we would like to thank National Center for High Perforamnce Computing and TWCC for providing the computing resources for this project.

Disclaimer